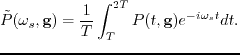Next: Born Modeling of a
Up: Theory
Previous: Single Frequency Response Modeling
Contents
All the shots in a supergather can propagate at the same time in the time domain,
![$\displaystyle (\bigtriangledown^{2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2...
...bf{x})=-\sum_{s}Re[W(\omega_{s})e^{i\omega_{s}t}]\delta(\textbf{x}-\textbf{s}).$](img149.png) |
(37) |
At the receiver locations, the observed time domain data
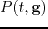 need to be transformed into the frequency domain and each shot selects the component according to its frequency encoding
need to be transformed into the frequency domain and each shot selects the component according to its frequency encoding
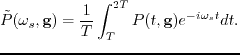 |
(38) |
In this case, the above integration should be carried out from 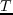 to
to 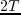 where
where
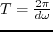 (Nihei and Li, 2006).
Digitizing
(Nihei and Li, 2006).
Digitizing
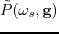 yields a supergather containing the blended full wavefields.
yields a supergather containing the blended full wavefields.
Wei Dai
2013-07-10
![$\displaystyle (\bigtriangledown^{2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2...
...bf{x})=-\sum_{s}Re[W(\omega_{s})e^{i\omega_{s}t}]\delta(\textbf{x}-\textbf{s}).$](img149.png)