Numerical Implementation

The numerical scheme in equation  is applicable to any migration method and its associated forward modeling (demigration) operator. Each type of migration method, e.g. Kirchhoff migration, one-way wave-equation migration or reverse time migration, can be implemented in the mode of least-squares migration (Nemeth et al., 1999; Duquet et al., 2000; Kaplan et al., 2010; Dai and Schuster, 2010; Dai et al., 2010). When combined with blended sources processing, each specific implementation will bear different advantages. 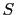The computational cost of the one-way wave-equation migration or reverse time migration method is reduced by $S$ times when 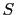$S$ sources are blended together. In addition, the I/O cost is reduced by 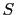$S$ times with static encoding method. On the other hand, the computational cost of Kirchhoff migration is relatively low, but it cannot be further reduced with blended sources processing because the Kirchhoff migration operation of $\textbf{L}^{T}_{i}\textbf{P}^{T}_{i}$ in equation must be applied separately to the supergather for $i=1,2,...,S$ . However, the I/O cost is reduced by inputting only a supergather so this will reduce the overall run time of Kirchhoff least-squares migration.

In this Chapter, the multisource least-squares migration algorithm is implemented with Kirchhoff migration and tested on synthetic blended sources data. To expedite convergence, a deblurring filter (see Appendix A) is used as a preconditioner (Hu and Schuster, 2000; Guitton, 2004; Aoki and Schuster, 2009) that can reduce the migration artifacts related to Kirchhoff migration (frowns and smiles) and compensate for the energy loss from geometric spreading; and therefore, speed up the convergence. Numerical simulations are conducted to validate these statements.