



Next: Plane-wave prestack LSRTM
Up: Theory
Previous: Theory
Contents
For conventional least-squares migration (Nemeth et al., 1999), a reflectivity model
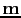 is assumed to be independent of the shot position. For a dataset with
is assumed to be independent of the shot position. For a dataset with 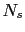 shots, the modeling process can be expressed as
shots, the modeling process can be expressed as
![$\displaystyle \begin{bmatrix}
\textbf{d}_1\\
\textbf{d}_2\\
\cdot\\
\tex...
...L}_2 \\
\cdot\\
\textbf{L}_{N_s}
\end{bmatrix}\left [ \textbf{m} \right ],$](img102.png) |
(24) |
and similarly for the migration
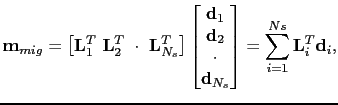 |
(25) |
where the final image is the stack of migration images from all of the individual shots.
For conventional least-squares migration, a reflectivity model
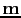 is sought that minimizes the misfit functional
is sought that minimizes the misfit functional
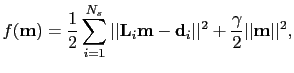 |
(26) |
where 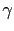 is the damping coefficient, and
is the damping coefficient, and
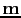 is defined as the stacked migration image. This method will also be referred as least-squares migration with the stacked image.
In Dai et al. (2012), the stacked migration image is computed from a blend of phase encoded shot gathers, also known as a supergather. When the migration velocity is not accurate, the prestack images are not exactly the same from different shots, and the stacked image can become blurred and convergence stalls.
is defined as the stacked migration image. This method will also be referred as least-squares migration with the stacked image.
In Dai et al. (2012), the stacked migration image is computed from a blend of phase encoded shot gathers, also known as a supergather. When the migration velocity is not accurate, the prestack images are not exactly the same from different shots, and the stacked image can become blurred and convergence stalls.
In order to improve the robustness of LSRTM, I define the ensemble of prestack images as a function of the shot position:
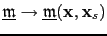 ,
or in matrix-vector notation
,
or in matrix-vector notation
 |
(27) |
where
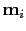 is the migration image for the
is the migration image for the 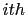 shot.
Now for a dataset with
shot.
Now for a dataset with 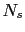 shots, the forward modeling operation is
shots, the forward modeling operation is
 |
(28) |
and the migration operation is
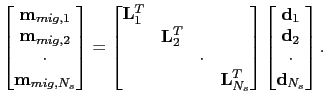 |
(29) |
For simplicity, I define
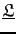 as the forward modeling operator for all the shot gathers
as the forward modeling operator for all the shot gathers
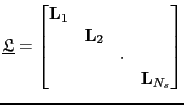 |
(30) |
and equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) and
and ![[*]](file:~/utilities/latex2html/icons/crossref.png) are rewritten in compact form
are rewritten in compact form
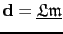 |
(31) |
and
 |
(32) |
Therefore, the misfit functional with the ensemble of prestack images is defined as
A preconditioned conjugate gradient algorithm
can be implemented to find the solution
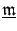 that minimizes the misfit in equation
that minimizes the misfit in equation ![[*]](file:~/utilities/latex2html/icons/crossref.png) . In above equation,
. In above equation,
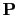 is the matrix representing the illumination compensation preconditioner (Plessix and Mulder, 2004).
is the matrix representing the illumination compensation preconditioner (Plessix and Mulder, 2004).
The ensemble of prestack images
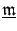 contains many more unknowns than the stacked image, and therefore provides more freedom to fit the observed data (see Appendix C). Another advantage is that the common image gathers can be extracted from the prestack images as an indication of the image quality.
contains many more unknowns than the stacked image, and therefore provides more freedom to fit the observed data (see Appendix C). Another advantage is that the common image gathers can be extracted from the prestack images as an indication of the image quality.




Next: Plane-wave prestack LSRTM
Up: Theory
Previous: Theory
Contents
Wei Dai
2013-07-10
![$\displaystyle \begin{bmatrix}
\textbf{d}_1\\
\textbf{d}_2\\
\cdot\\
\tex...
...L}_2 \\
\cdot\\
\textbf{L}_{N_s}
\end{bmatrix}\left [ \textbf{m} \right ],$](img102.png)
![$\displaystyle \begin{bmatrix}
\textbf{d}_1\\
\textbf{d}_2\\
\cdot\\
\tex...
...L}_2 \\
\cdot\\
\textbf{L}_{N_s}
\end{bmatrix}\left [ \textbf{m} \right ],$](img102.png)
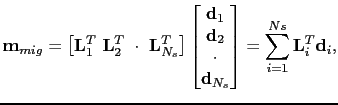
![]() is sought that minimizes the misfit functional
is sought that minimizes the misfit functional
![]() ,
or in matrix-vector notation
,
or in matrix-vector notation


![]() and
and ![]() are rewritten in compact form
are rewritten in compact form
![]() contains many more unknowns than the stacked image, and therefore provides more freedom to fit the observed data (see Appendix C). Another advantage is that the common image gathers can be extracted from the prestack images as an indication of the image quality.
contains many more unknowns than the stacked image, and therefore provides more freedom to fit the observed data (see Appendix C). Another advantage is that the common image gathers can be extracted from the prestack images as an indication of the image quality.