Theory
I now present the spectral encoding strategy for removing crosstalk artifacts in multisource imaging.
First, I identify the source spectrum in the forward modeling equation. Then,
I outline a typical phase-encoded multisource procedure, before developing the proposed frequency encoding method.
In the frequency domain a seismic trace with a source at
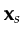 and a receiver at
and a receiver at  can be
expressed (Stolt and Benson, 1986), based on the Born approximation to the Lippman-Schwinger equation, as
can be
expressed (Stolt and Benson, 1986), based on the Born approximation to the Lippman-Schwinger equation, as
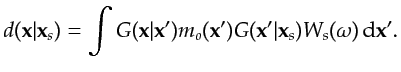 |
(2.1) |
Here,
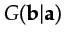 denotes the Green's function from
denotes the Green's function from 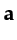 to
to 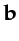 ;
;
 is the reflection coefficient-like term at
is the reflection coefficient-like term at
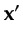 ,
where
,
where
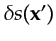 is the slowness perturbation from an assumed
background slowness
is the slowness perturbation from an assumed
background slowness
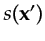 ; and
Ws is the spectrum of the
; and
Ws is the spectrum of the
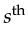 source weighted
by
source weighted
by
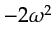 and can be
pulled outside the integral since it is independent of
and can be
pulled outside the integral since it is independent of
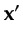 .
For conciseness
.
For conciseness
 is hereafter referred to as `source spectrum' or simply
`spectrum' for short. As the earth model is discretized into
is hereafter referred to as `source spectrum' or simply
`spectrum' for short. As the earth model is discretized into 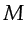 grid points,
equation 2.1 can be recast in matrix-vector form as
grid points,
equation 2.1 can be recast in matrix-vector form as
Here,
 is the reflectivity model;
is the reflectivity model;
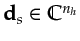 represents the
represents the
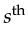 shot gather;
S is the number of shots;
nh is the number of receivers per shot;
shot gather;
S is the number of shots;
nh is the number of receivers per shot;
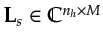 represents the prestack modeling operator for the
represents the prestack modeling operator for the
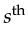 shot gather, and
shot gather, and
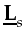 is
Ls deprived of Ws.
Equations 2.2 to 2.4 are in the frequency domain and
recognize that quantities such as
is
Ls deprived of Ws.
Equations 2.2 to 2.4 are in the frequency domain and
recognize that quantities such as
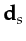 ,
,
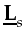 , and
, and
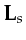 all depend on
all depend on 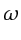 , which is silent to reduce
notational clutter; however,
, which is silent to reduce
notational clutter; however, 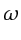 is explicitly retained in
is explicitly retained in
 ,
because
,
because
 represents the proposed frequency encoding function.
Note also the subscript in
represents the proposed frequency encoding function.
Note also the subscript in
 , implying that different sources may have different spectrums.
, implying that different sources may have different spectrums.
Subsections
Yunsong Huang
2013-09-22
![]() and a receiver at
and a receiver at ![]() can be
expressed (Stolt and Benson, 1986), based on the Born approximation to the Lippman-Schwinger equation, as
can be
expressed (Stolt and Benson, 1986), based on the Born approximation to the Lippman-Schwinger equation, as
 is the reflection coefficient-like term at
is the reflection coefficient-like term at