While existing approaches such as studied by Schuster et al. (2011) strive to reduce the crosstalk noise by devising phase encoding functions such that
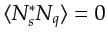 for
for 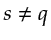 ,
this chapter relies on devising source spectra
,
this chapter relies on devising source spectra
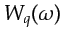 's in order to eliminate the noise term
's in order to eliminate the noise term  defined in equation 2.15. To this end, I single out an arbitrary term in equation 2.15 and investigate how to
make it zero. An example of such a term is expressed as
defined in equation 2.15. To this end, I single out an arbitrary term in equation 2.15 and investigate how to
make it zero. An example of such a term is expressed as
Because the dependence of
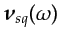 on
on 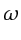 is typically spatially varying and unknown,
it is impossible to construct
is typically spatially varying and unknown,
it is impossible to construct
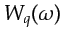 's that can suppress
all elements of
's that can suppress
all elements of
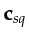 , unless the source spectra are non-overlapping.
Non-overlapping source spectra ensure that
, unless the source spectra are non-overlapping.
Non-overlapping source spectra ensure that
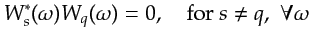 |
(2.19) |
and in turn reduce equation 2.15 to zero.
I refer to this encoding scheme as frequency selection.
The previous analysis contrasts the different roles that the phase encoder
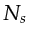 and frequency encoder
and frequency encoder
 play. For notational economy, however,
hereafter
in the context of frequency selection I recast
play. For notational economy, however,
hereafter
in the context of frequency selection I recast 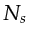 as a frequency encoder, on which
as a frequency encoder, on which
 is predicated;
in addition, omega is discretized, and is identified
with a frequency index j running from 1 to nomega. The frequency encoder is given as
a binary vector
is predicated;
in addition, omega is discretized, and is identified
with a frequency index j running from 1 to nomega. The frequency encoder is given as
a binary vector
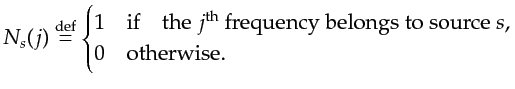 |
(2.20) |
Note that
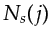 's are no longer of pure phase; this can be regarded as a form of amplitude encoding (Godwin and Sava, 2010).
If no frequency index is shared by multiple sources,
then equation 2.20 leads to
's are no longer of pure phase; this can be regarded as a form of amplitude encoding (Godwin and Sava, 2010).
If no frequency index is shared by multiple sources,
then equation 2.20 leads to
 |
(2.21) |
Thus equation 2.19 is guaranteed, in my new notation, by the choice
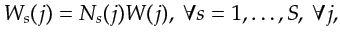 |
(2.22) |
where  is the intact source spectrum.
In shorthand, equation 2.21 can be expressed as
is the intact source spectrum.
In shorthand, equation 2.21 can be expressed as
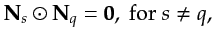 |
(2.23) |
where 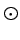 represents element-wise multiplication between two vectors.
If, moreover, every frequency index is assigned to some source, then
equation 2.20 leads to
represents element-wise multiplication between two vectors.
If, moreover, every frequency index is assigned to some source, then
equation 2.20 leads to
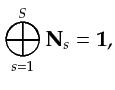 |
(2.24) |
where 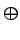 represents element-wise addition.
Accordingly, following equation 2.22, we have
represents element-wise addition.
Accordingly, following equation 2.22, we have
Given 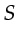 sources and
sources and 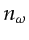 frequency indices, frequency selection endeavors to evenly divide the latter among the former. That is, on average each source is assigned
frequency indices, frequency selection endeavors to evenly divide the latter among the former. That is, on average each source is assigned
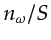 frequency indices.
frequency indices.
I outline next how 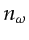 is determined.
Suppose the maximal travel time between sources
and their associated receivers is
is determined.
Suppose the maximal travel time between sources
and their associated receivers is 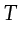 , the peak frequency of the source wavelet is
, the peak frequency of the source wavelet is 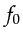 , and the cutoff high
frequency is at
, and the cutoff high
frequency is at
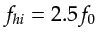 . The Nyquist sampling theorem dictates
. The Nyquist sampling theorem dictates
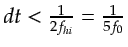 , and therefore the total number of time samples is
, and therefore the total number of time samples is
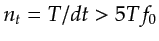 . For real signals devoid of dc, the number of independent angular frequencies
is given by
. For real signals devoid of dc, the number of independent angular frequencies
is given by
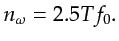 |
(2.27) |
For example, the parameters chosen for my 2D and 3D simulations are:
 as
as 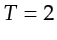 s and
s and 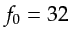 Hz, and
Hz, and
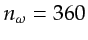 as
as 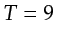 s and
s and 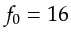 Hz, respectively.
Note that the effective number of independent frequencies is smaller than
Hz, respectively.
Note that the effective number of independent frequencies is smaller than 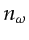 , because the
source spectrum
, because the
source spectrum  is far from uniform.
is far from uniform.
Yunsong Huang
2013-09-22
![]() is determined.
Suppose the maximal travel time between sources
and their associated receivers is
is determined.
Suppose the maximal travel time between sources
and their associated receivers is ![]() , the peak frequency of the source wavelet is
, the peak frequency of the source wavelet is ![]() , and the cutoff high
frequency is at
, and the cutoff high
frequency is at
![]() . The Nyquist sampling theorem dictates
. The Nyquist sampling theorem dictates
![]() , and therefore the total number of time samples is
, and therefore the total number of time samples is
![]() . For real signals devoid of dc, the number of independent angular frequencies
is given by
. For real signals devoid of dc, the number of independent angular frequencies
is given by