Next: Method Up: Eliminating Marine Acquisition Crosstalk Previous: Eliminating Marine Acquisition Crosstalk Contents
Let I/O cost be identified with the size2.3 of data passing through I/O,
and assume the data size is ![]() .
The standard migration entails reading every shot gather, followed by the Fourier transform and then the migration.
So the I/O cost is
.
The standard migration entails reading every shot gather, followed by the Fourier transform and then the migration.
So the I/O cost is
![]() . On the other hand, the work flow of the proposed method consists of two stages.
(1) Preparation. All input data are read, transformed to the frequency domain and saved to disk.
The I/O cost of this stage is
. On the other hand, the work flow of the proposed method consists of two stages.
(1) Preparation. All input data are read, transformed to the frequency domain and saved to disk.
The I/O cost of this stage is
![]() .
(2) Migration. The I/O cost per iteration is
.
(2) Migration. The I/O cost per iteration is
![]() .
In
.
In ![]() iterations, the I/O cost
is
iterations, the I/O cost
is
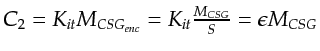 , where
, where
![]() as
as
![]() is typically an order of magnitude smaller than
is typically an order of magnitude smaller than ![]() , which is how speedup can be gained by iterative multisource methods.
Therefore the I/O cost
, which is how speedup can be gained by iterative multisource methods.
Therefore the I/O cost
![]() of the proposed method is a little more than twice that of
the standard approach for any
of the proposed method is a little more than twice that of
the standard approach for any
![]() . If the data is in the frequency domain already, then the work pertaining to stage (1)
is unnecessary. In this case, the I/O cost of the proposed method is only
. If the data is in the frequency domain already, then the work pertaining to stage (1)
is unnecessary. In this case, the I/O cost of the proposed method is only
![]() .
.
If
![]() can fit in a computer's memory,
can fit in a computer's memory, ![]() can be further reduced as follows.
Read the CSGs from disk to form a
can be further reduced as follows.
Read the CSGs from disk to form a
![]() , which is kept in the memory, then make
, which is kept in the memory, then make ![]() iterative updates2.4 to the trial model.
In this scheme,
iterative updates2.4 to the trial model.
In this scheme, ![]() is reduced by a factor2.5 of
is reduced by a factor2.5 of ![]() .
.