Once sources have been assigned non-overlapping sets of frequencies, marine acquisition crosstalk can
be eliminated.
The key idea is, after completing multisource forward modeling by computer simulation,
at each receiver 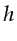 any extraneous frequency component
any extraneous frequency component 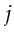 is pruned;
is pruned; 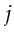 is considered extraneous
if
is considered extraneous
if 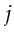 is assigned to a source, to which, according to the marine geometry,
is assigned to a source, to which, according to the marine geometry, 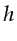 is not associated.
I illustrate the proposed algorithm with an example shown in Figure 2.1.
Figure 2.1(a) depicts
is not associated.
I illustrate the proposed algorithm with an example shown in Figure 2.1.
Figure 2.1(a) depicts 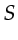 =3 sources,
=3 sources, 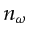 =5 frequencies,
and a specific way of frequency selection described by the frequency encoders
=5 frequencies,
and a specific way of frequency selection described by the frequency encoders 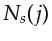 's identified as, from left
to right,
's identified as, from left
to right,
![$ N_3=[1,0,0,0,1]^T$](img162.png) ,
,
![$ N_2=[0,1,0,0,0]^T$](img163.png) , and
, and
![$ N_1=[0,0,1,1,0]^T$](img164.png) .
Figure 2.1(b) depicts a towed marine geometry, where
each source is associated with
.
Figure 2.1(b) depicts a towed marine geometry, where
each source is associated with
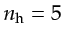 receivers. For instance,
source
receivers. For instance,
source 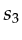 is associated with receivers
is associated with receivers 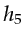 -
-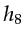 ,
but not with receivers
,
but not with receivers 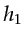 -
-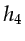 . Consider for example
. Consider for example 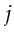 =5 at receiver
=5 at receiver 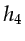 .
Because, according to Figure 2.1(a),
.
Because, according to Figure 2.1(a), 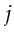 =5 is assigned to source
=5 is assigned to source 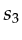 ,
,
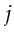 =5 is considered extraneous at receivers
=5 is considered extraneous at receivers 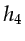 and should be pruned.
The rationale is as follows. When sources are blended, all frequency components are present (see equation 2.26)
in forward modeling and consequently at every receiver. Receiver
and should be pruned.
The rationale is as follows. When sources are blended, all frequency components are present (see equation 2.26)
in forward modeling and consequently at every receiver. Receiver 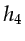 would
have detected frequency component 5, which comes from source
would
have detected frequency component 5, which comes from source 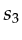 , but
, but 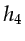 lies outside the
aperture associated to
lies outside the
aperture associated to 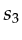 , and therefore
, and therefore 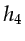 should not pick up any signal stemming from
should not pick up any signal stemming from 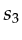 .
This explains the pruning of the extraneous frequency component 5 at
.
This explains the pruning of the extraneous frequency component 5 at 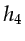 .
This is indicated by the absence of a bar corresponding to
.
This is indicated by the absence of a bar corresponding to 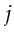 =5 at
=5 at 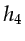 in Figure 2.1(c). Other unoccupied frequency slots in Figure 2.1(c) are likewise inferred.
in Figure 2.1(c). Other unoccupied frequency slots in Figure 2.1(c) are likewise inferred.
The pruning operation is equivalent to selective filling in as follows.
Let F_blen(frequency, receiver) of size
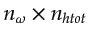 be the outcome2.1in the frequency domain detected by receivers
generated by forward modeling with blended sources prior to pruning, and let F_prun(frequency, receiver)
of the same size
be the result of pruning applied to F_blen. Here,
be the outcome2.1in the frequency domain detected by receivers
generated by forward modeling with blended sources prior to pruning, and let F_prun(frequency, receiver)
of the same size
be the result of pruning applied to F_blen. Here, 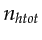 is the total number of
receivers covered by the supergather, and
is the total number of
receivers covered by the supergather, and
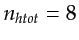 in this example. F_prun is obtained by first
initialization with 0 and subsequently filling in with valid entries in F_blen; an entry
F_blen(
in this example. F_prun is obtained by first
initialization with 0 and subsequently filling in with valid entries in F_blen; an entry
F_blen(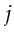 ,
, 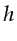 ) is valid if frequency component
) is valid if frequency component 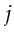 is not extraneous at receiver
is not extraneous at receiver 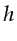 .
For instance for
.
For instance for 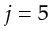 , we have
, we have
![$\displaystyle \ce{F_{prun}}(j=5,[h_5,h_6,h_7,h_8]) \gets \ce{F_{blen}}(j=5,[h_5,h_6,h_7,h_8])$](img178.png) |
(2.28) |
Similarly, the encoded supergather
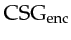 , of size
, of size
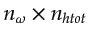 , can be formed
as follows, assuming that the
observed csg have been transformed to the frequency domain and are indexed as
CSG(frequency, receiver, source), of size
, can be formed
as follows, assuming that the
observed csg have been transformed to the frequency domain and are indexed as
CSG(frequency, receiver, source), of size
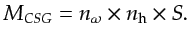 |
(2.29) |
Here, nh is the number of receivers associated with each source in acquisition, and
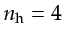 in this example.
First,
in this example.
First,
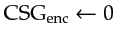 . Next, fill in
. Next, fill in
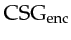 with the corresponding entries in CSG according to the current frequency encoders.
Specifically, loop j over nomega,
and for a given
with the corresponding entries in CSG according to the current frequency encoders.
Specifically, loop j over nomega,
and for a given 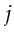 , find to which source
, find to which source 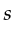 it belongs, and subsequently find which receivers
it belongs, and subsequently find which receivers 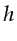 's
are associated to this
's
are associated to this 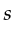 . Then execute
. Then execute
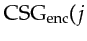 ,
, 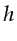 's)
's) 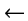 CSG(
CSG(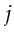 , :,
, :, 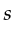 ).
An example for
).
An example for 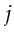 =3 is given as
=3 is given as
Finally, the misfit function is computed by
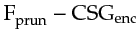 .
By pruning or equivalently selective filling in, the mismatch problem between the limited number,
.
By pruning or equivalently selective filling in, the mismatch problem between the limited number, 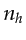 , of live traces/shot in observed CSG, and the pervasive number,
, of live traces/shot in observed CSG, and the pervasive number, 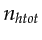 , of traces in simulation-generated F_blen
is now resolved.
, of traces in simulation-generated F_blen
is now resolved.
Note that since there are 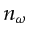 equations similar to equation 2.30, each reading
equations similar to equation 2.30, each reading 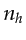 entries,
the total number of entries read from CSG by selective filling in is
entries,
the total number of entries read from CSG by selective filling in is
In this example
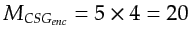 , coinciding with the number of bars in
Figure 2.1(c).
, coinciding with the number of bars in
Figure 2.1(c).
Subsections
Yunsong Huang
2013-09-22
![\includegraphics[width=4.5in]{fig/Freq_selec_marine}](img173.png)
![]() be the outcome2.1in the frequency domain detected by receivers
generated by forward modeling with blended sources prior to pruning, and let F_prun(frequency, receiver)
of the same size
be the result of pruning applied to F_blen. Here,
be the outcome2.1in the frequency domain detected by receivers
generated by forward modeling with blended sources prior to pruning, and let F_prun(frequency, receiver)
of the same size
be the result of pruning applied to F_blen. Here, ![]() is the total number of
receivers covered by the supergather, and
is the total number of
receivers covered by the supergather, and
![]() in this example. F_prun is obtained by first
initialization with 0 and subsequently filling in with valid entries in F_blen; an entry
F_blen(
in this example. F_prun is obtained by first
initialization with 0 and subsequently filling in with valid entries in F_blen; an entry
F_blen(![]() ,
, ![]() ) is valid if frequency component
) is valid if frequency component ![]() is not extraneous at receiver
is not extraneous at receiver ![]() .
For instance for
.
For instance for ![]() , we have
, we have
![]() equations similar to equation 2.30, each reading
equations similar to equation 2.30, each reading ![]() entries,
the total number of entries read from CSG by selective filling in is
entries,
the total number of entries read from CSG by selective filling in is