The fwimfs is then tested on a gom streamer dataset. I include 496 shots with a shot interval of 37.5 m. The source-receiver offset ranges from 198 m to 6 km, with a receiver spacing of 12.5 m. Trace length of 7 s is included, with a sampling interval of 2 ms.
This test consists of the following steps:
- Estimate the source wavelet, by integrating the direct wave.
- Convert the 3D physical data to 2D, on which grid the simulations are run.
- Obtain an initial velocity model, shown in Figure 3.9(a), by combining traveltime tomography and the velocity from semblance analysis, referred in short in this chapter simply as `traveltime tomography'.
- Implement a multiscale strategy (Bunks et al., 1995) with fwimfs.
- To validate the accuracy of the tomogram, compute the RTM image and cig using the tomogram velocity.
Figure 3.6:
The direct wave and free-surface reflection combine together to give a detected signal approximated
by
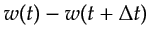 , proportional to the time derivative of the wavelet w(t).
, proportional to the time derivative of the wavelet w(t).
|
![\includegraphics[width=2.5in]{fwi_fig/SrcWvlt_freeSurf_ghost}](img309.png) |
Figure 3.7:
(a) The estimated source wavelet, (b) bandpass filtered wavelet with peak frequency 10 Hz.
(c) The power spectrum of (b), which is divided into intervals in order to make the energy of each interval comparable.
(Due to discreteness of frequencies, the interval energy cannot be made exactly equal.)
|
![\includegraphics[width=5.9in]{fwi_fig/src_wvlt_freq_divi}](img310.png) |
The source wavelet is estimated as follows. 1) Stack the direct waves from cog;
2) integrate the stacked trace along time;
and 3) set its dc component to 0. The reason for integration is because the received direct wave
is
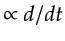 of the source wavelet, as illustrated in Figure 3.6.
The estimated source wavelet is plotted in Figure 3.7(a); a bandpass filtered version
(filtered with a Ricker wavelet of peak frequency 10 Hz) is plotted in Figure 3.7(b).
There are 210 frequency components supporting the power spectrum curve plotted in Figure 3.7(c).
As the power is very small at the tails, rather than assigning each frequency component individually,
I group them into 62 frequency intervals, filled in alternating colors in Figure 3.7(c).
The intervals are wider near the tails, so that the area under the curve in each
interval is equalized as best as one can.
Each interval of frequencies is selected as
one entity in my frequency-selection scheme.
The 3D to 2D conversion is achieved by multiplying the data spectra by
of the source wavelet, as illustrated in Figure 3.6.
The estimated source wavelet is plotted in Figure 3.7(a); a bandpass filtered version
(filtered with a Ricker wavelet of peak frequency 10 Hz) is plotted in Figure 3.7(b).
There are 210 frequency components supporting the power spectrum curve plotted in Figure 3.7(c).
As the power is very small at the tails, rather than assigning each frequency component individually,
I group them into 62 frequency intervals, filled in alternating colors in Figure 3.7(c).
The intervals are wider near the tails, so that the area under the curve in each
interval is equalized as best as one can.
Each interval of frequencies is selected as
one entity in my frequency-selection scheme.
The 3D to 2D conversion is achieved by multiplying the data spectra by
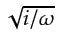 (Barton, 1989)
and then gaining in the time domain by
(Barton, 1989)
and then gaining in the time domain by 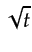 to convert the geometric spreading from 3D to 2D.
to convert the geometric spreading from 3D to 2D.
Subsections
Yunsong Huang
2013-09-22
![\includegraphics[width=2.5in]{fwi_fig/SrcWvlt_freeSurf_ghost}](img309.png)
![\includegraphics[width=5.9in]{fwi_fig/src_wvlt_freq_divi}](img310.png)
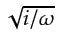 (Barton, 1989)
and then gaining in the time domain by
(Barton, 1989)
and then gaining in the time domain by