As shown in Figures 3.9(b) and (c), the tomograms computed by standard FWI after 20 iterations and
by FWIMFS after 71 iterations appear very similar. The associated computational cost of the latter case is 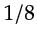 of that of the former.
In both cases, there appear to be some regions of low-velocity anomalies.
One is a horizontal layer at a depth of 0.75 km, where the velocity is slower than in water.
This could be due to out-of-plane wavepaths modeled in 2D, resulting in underestimating the velocity,
or it indicates unconsolidated sediments.
Other low-velocity anomalies seem to lie along the wavepaths of diving waves.
This arises due to cycle-skipping of some of the diving waves. Such velocities can be elevated by manual intervention,
a trial move to be accepted if it overcomes some cycle-skipping. Rather than going into details of improving the FWI results,
this chapter aims at demonstrating that FWIMFS produces essentially the same results as standard FWI does, with the benefit of a
reduction in the computational cost. How we massage the velocity model to address the cycle-skipping is a separate research project.
of that of the former.
In both cases, there appear to be some regions of low-velocity anomalies.
One is a horizontal layer at a depth of 0.75 km, where the velocity is slower than in water.
This could be due to out-of-plane wavepaths modeled in 2D, resulting in underestimating the velocity,
or it indicates unconsolidated sediments.
Other low-velocity anomalies seem to lie along the wavepaths of diving waves.
This arises due to cycle-skipping of some of the diving waves. Such velocities can be elevated by manual intervention,
a trial move to be accepted if it overcomes some cycle-skipping. Rather than going into details of improving the FWI results,
this chapter aims at demonstrating that FWIMFS produces essentially the same results as standard FWI does, with the benefit of a
reduction in the computational cost. How we massage the velocity model to address the cycle-skipping is a separate research project.
Figure 3.9:
FWI results for the gom dataset. (a) The initial velocity model.
The velocity tomograms obtained from (b) standard FWI after 20 iteration steps, and
(c) fwimfs after 71 iteration steps. The encircled regions are low velocity anomalies in the FWI results.
|
![\includegraphics[width=6in]{fwi_fig/FWI_tomograms}](img334.png) |
Figure 3.10:
Difference of FWI velocity models obtained using Quasi-Monte Carlo versus standard random permutation in frequency-selection encoding.
The encirclements are for reference only.
|
![\includegraphics[width=6in]{fwi_fig/FWI_diff}](img335.png) |
In order to see how my quasi-Monte Carlo encoding scheme accelerates the inversion,
Figure 3.10 shows the velocity differences between the tomograms
obtained using the two alternative encoding schemes: standard random permutation versus quasi-Monte Carlo.
Surprisingly, the two velocity models are almost identical.
The other results, such as RTM images and CIGs, appear indistinguishable, and therefore further comparisons between the two are omitted.
This implies that the FWIMFS is very robust with regard to specific random codes of frequency-selection.
Figure 3.11 plots the convergence curves of the various approaches. The reason why the red curve lies
slightly above the green one is explained as follows. By quasi-Monte Carlo encoding, the new multisource data presented to the inversion algorithm is
very different from what it has seen in the past, because this data contains entirely new frequency components.
In contrast, by standard random permutation, some frequency components may have been used earlier, and
thus the new multisource data is not entirely new. So the algorithm using standard random permutation
can fare better at fitting the data.
Figure 3.11:
Reduction of data misfit (for 0-25 Hz) over FWI iterations, starting from the model obtained from FWI of 0-15 Hz data.
The iteration numbers are labeled according to those of the standard FWI (i.e., of individual-source).
The curves of the multisource cases are scaled horizontally such that when one draws a vertical line across this figure,
the intersected red and green points represent 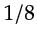 of the computational cost than the cost of the intersected blue point.
of the computational cost than the cost of the intersected blue point.
|
![\includegraphics[width=5in]{fwi_fig/Baldplate_dataErr_cnvrgCurves}](img336.png) |
To probe the qualities of FWI, RTM images are shown in Figure 3.12, with zoomed views shown in Figure 3.13.
Note that the results of standard FWI and of FWIMFS appear identical. In the three zoomed views, the FWI results seem more focused,
showing better continuity of reflectors. In the center of the RTM images, around
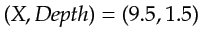 km, however, the traveltime tomogram
offers better focusing than FWI tomograms. This is perhaps due to the overhanging low velocity anomalies in the FWI tomograms,
as remarked on Figure 3.9.
km, however, the traveltime tomogram
offers better focusing than FWI tomograms. This is perhaps due to the overhanging low velocity anomalies in the FWI tomograms,
as remarked on Figure 3.9.
Figure 3.13:
Zoomed views of the RTM images in Figure 3.12.
|
![\includegraphics[width=6in]{fwi_fig/zoomed_views}](img341.png) |
Figure 3.14:
Shot domain cig. The boxed areas show improved flatness in the FWI results compared to that of the traveltime tomogram.
|
![\includegraphics[width=6in]{fwi_fig/CIGs}](img342.png) |
Comparing the CIGs in Figure 3.14, we see flatter events on the right part, delimited by the red box.
This coincides with the observations about the RTM images in that the FWI results fare better (in terms of more focused
and continual reflectors) on the right part of the RTM image. In the green box of the CIGs, although the FWI results are flatter than
the traveltime counterpart, the FWI velocity is over-corrected to be too small.
This is indicated by the events curving up with larger source-midpoint offset (larger offset is on the left side of each CIG strip).
This supports the idea that the overhanging low velocity anomalies are not authentic.
Figure 3.15:
csg for GOM data of one source at 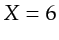 km. (a) the observed data bandpass filtered to 0-25 Hz.
The predicted counterparts obtained with the (b) traveltime tomograms, (c) standard FWI (after 20 iterations), and (d) FWIMFS (after 71 iterations).
km. (a) the observed data bandpass filtered to 0-25 Hz.
The predicted counterparts obtained with the (b) traveltime tomograms, (c) standard FWI (after 20 iterations), and (d) FWIMFS (after 71 iterations).
|
![\includegraphics[width=6in]{fwi_fig/CSG1s}](img343.png) |
Figures 3.15 and 3.16 show CSGs from two sources, obtained by various methods.
The match between the FWI results and the observed ones is generally good, although
cycle skipping can be found at offsets  km and 6 km, while comparing panels (a) and (c) in Figure 3.15.
km and 6 km, while comparing panels (a) and (c) in Figure 3.15.
Figure 3.16:
csg for GOM data of one source at 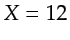 km. (a) the observed data bandpass filtered to 0-25 Hz.
The predicted counterparts obtained with the (b) traveltime tomograms, (c) standard FWI (after 20 iterations), and (d) FWIMFS (after 71 iterations).
km. (a) the observed data bandpass filtered to 0-25 Hz.
The predicted counterparts obtained with the (b) traveltime tomograms, (c) standard FWI (after 20 iterations), and (d) FWIMFS (after 71 iterations).
|
![\includegraphics[width=6in]{fwi_fig/CSG2s}](img345.png) |
Yunsong Huang
2013-09-22
![\includegraphics[width=6in]{fwi_fig/FWI_tomograms}](img334.png)
![\includegraphics[width=6in]{fwi_fig/FWI_diff}](img335.png)
![\includegraphics[width=5in]{fwi_fig/Baldplate_dataErr_cnvrgCurves}](img336.png)
![\begin{subfigure}[b]{6in}
\centering
\includegraphics[width=6in]{fwi_fig/RTM_tomo}
\end{subfigure}](img337.png)
![\begin{subfigure}[b]{6in}
\centering
\includegraphics[width=6in]{fwi_fig/RTM_fwi}
\end{subfigure}](img338.png)
![\begin{subfigure}[b]{6in}
\centering
\includegraphics[width=6in]{fwi_fig/RTM_fwi_ms_u}
\end{subfigure}](img339.png)
![]() km, however, the traveltime tomogram
offers better focusing than FWI tomograms. This is perhaps due to the overhanging low velocity anomalies in the FWI tomograms,
as remarked on Figure 3.9.
km, however, the traveltime tomogram
offers better focusing than FWI tomograms. This is perhaps due to the overhanging low velocity anomalies in the FWI tomograms,
as remarked on Figure 3.9.
![\includegraphics[width=6in]{fwi_fig/CIGs}](img342.png)
![\includegraphics[width=6in]{fwi_fig/CSG1s}](img343.png)
![\includegraphics[width=6in]{fwi_fig/CSG2s}](img345.png)