Resolution Limits for Traveltime Tomography

In raypath traveltime tomography, the velocity is updated only along the raypath that connects the source at ${\bf {s}}$ with the receiver at ${\bf {g}}$ , whereas in finite-frequency traveltime tomography, velocity updates can be confined to the first Fresnel zone for the specified source-receiver pair (Harlan, 1990). He states ``....band-limited waves can follow paths that are not Fermat raypaths and still cover the distance between two points in almost the same time. All arriving waves that are delayed by less than half a wavelength will add constructively to the first arrival.''

As an example, the raypaths and Fresnel zones for reflection and transmission arrivals are illustrated in Figure 4.1. A point ${\bf {x}}$ is in the Fresnel zone (FZ) if and only if it satisfies the following condition (Kravtsov and Orlov, 1990; Cerveny and Soares, 1992):

$$\vert\tau_{sx} + \tau_{xg} - \tau_{sg}\vert \leq T/2,$$ (4.1)

where, $T$ is the dominant period of the source wavelet, $\tau_{sx}$ is the traveltime for a particular type of wave to propagate from ${\bf {s}}$ to the trial image point at ${\bf {x}}$ , and $\tau_{sg}$ is the traveltime to propagate from ${\bf {s}}$ to the specified geophone at ${\bf {g}}$ .

In a homogeneous medium, the maximum width of the first Fresnel zone can be shown (Williamson, 1991) to be proportional to 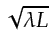$\sqrt{\lambda L}$ , where $L$ is the source-receiver distance and $\lambda$ is the dominant wavelength. Thus, widening the distance between the source and receiver lowers the spatial resolution of the traveltime tomogram. More generally, Appendix E derives the formula for the length between any two points on opposite sides of the ellipse, which provides the horizontal resolution limit for any orientation of the ellipse.

Figure 4.1: a) First-Fresnel zones for the specular reflection and for the transmission arrival excited by the mirror source at (0,2d). In the latter case, the velocity below the reflector has been extended to be the same as the top-layer velocity. b) An ellipse intersected by a line segment $DE$ , where its length $\overline{DE}= \frac{2ab\sqrt{b^2\cos^2\theta + (a^2-c^2)\sin^2\theta }} {b^2\cos^2\theta + a^2\sin^2\theta}$ defines the resolution limit (see Appendix E).

The effective spatial resolution limits $\Delta x$ and $\Delta z$ of traveltime tomograms can be estimated (Schuster, 1996) as the minimum width and height of the intersection of first Fresnel zones at the trial image point. As an example, Figure 4.2 shows the intersection zones for both a) reflection and b) transmission rays. At any point on the central raypath, the narrowest width is along the line perpendicular to this ray, which also defines the direction of best resolution. Thus, a horizontal ray gives the best vertical resolution while a vertically oriented ray provides the best horizontal resolution for transmission tomography, where the velocity is updated by smearing residuals along the first FZ (also referred to as a wavepath). As will be shown in the next section, this rule of thumb is also true for transmission wavepaths in FWI tomograms, except the $waveform~residual$ is smeared along the associated wavepath.

Figure 4.2: Same as Figure 4.1 except there is a new source (red star) along with its red wavepath for each diagram. The minimum width and height of the red-shaded intersection zone defines, respectively, the effective horizontal $\Delta x$ and vertical $\Delta z$ resolution limits of the traveltime tomogram at the yellow-filled circle.