Crosstalk in the communications industry is defined in
the online Merriam-Webster dictionary as ``unwanted signals in a
communication channel (as in a telephone, radio, or computer) caused
by transference of energy from another circuit (as by leakage or coupling).''
As we sometimes discover with analog phones, crosstalk can take the form of hearing
someone else's conversation  instead of hearing the
intended signal
instead of hearing the
intended signal 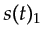 .
Mathematically the noisy signal
.
Mathematically the noisy signal 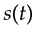 can be represented by
can be represented by
where additive random noise can also be considered.
Sometimes,  is also considered signal, and the efficient transmission
of both signals requires that they both be simultaneously transmitted,
but should be separated from one another after recording1.1.
To achieve this feat, the two signals are encoded and summed together to give
is also considered signal, and the efficient transmission
of both signals requires that they both be simultaneously transmitted,
but should be separated from one another after recording1.1.
To achieve this feat, the two signals are encoded and summed together to give
![$ s(t)'=F[s(t)_1]+F[s(t)_2]$](img39.png) prior to transmission,
and then decoded
to get the separate signals
prior to transmission,
and then decoded
to get the separate signals
![$ F_1^{-1}[s(t)'] =s(t)_1$](img40.png) and
and
![$ F_2^{-1}[s(t)'] =s(t)_2$](img41.png) .
This efficient means of simultaneously transmitting two signals and their
subsequent decoding is a monumental achievement
because it greatly reduces both the
cost and the number of channels required for today's multi-channel communication.
.
This efficient means of simultaneously transmitting two signals and their
subsequent decoding is a monumental achievement
because it greatly reduces both the
cost and the number of channels required for today's multi-channel communication.
The decoder 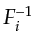 is a device or operation1.2 that does
the reverse of the
is a device or operation1.2 that does
the reverse of the  channel encoder, undoing the encoding so
that the original information can be retrieved.
An example in
digital electronics is where
a decoder can take the form of a multiple-input,
multiple-output logic circuit that
converts coded inputs into coded outputs.
Decoding is also necessary in applications such as data multiplexing,
which is seen in the oil industry with transmission
of multichannel seismic data.
channel encoder, undoing the encoding so
that the original information can be retrieved.
An example in
digital electronics is where
a decoder can take the form of a multiple-input,
multiple-output logic circuit that
converts coded inputs into coded outputs.
Decoding is also necessary in applications such as data multiplexing,
which is seen in the oil industry with transmission
of multichannel seismic data.
A more geophysically relevant model of crosstalk is
to include correlation terms that must be eliminated, i.e.,
where 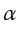 is a scalar weighting term, and
is a scalar weighting term, and 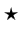 denotes correlation.
For our purposes, one might think of two shot gathers summed together
and simultaneously migrated to give the desirable sum of the individual migration images
denotes correlation.
For our purposes, one might think of two shot gathers summed together
and simultaneously migrated to give the desirable sum of the individual migration images
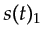 and
and  , and the undesirable crosstalk noise
, and the undesirable crosstalk noise
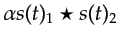 .
Similar to the benefits in the communications industry, Morton and Ober (1998)
and Romero et al. (2000) tested the possibility
of simultaneously migrating a sum of encoded shot gathers (herewith known
as a supergather)
to tremendously reduce computation
time and memory+I/O demands.
Unfortunately,
their early results did not show significant efficiencies
because
their method did not
easily annihilate the
crosstalk term
.
Similar to the benefits in the communications industry, Morton and Ober (1998)
and Romero et al. (2000) tested the possibility
of simultaneously migrating a sum of encoded shot gathers (herewith known
as a supergather)
to tremendously reduce computation
time and memory+I/O demands.
Unfortunately,
their early results did not show significant efficiencies
because
their method did not
easily annihilate the
crosstalk term
 .
.
In fact, decoding is mathematically simpler in the frequency domain where
equation 1.2 at 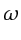 is given by
is given by
where
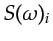 is the Fourier transform of
is the Fourier transform of 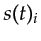 .
This frequency domain representation presents the opportunity
for decoding encoded signals by fdm,
where interfering signals are transmitted in several non-overlapping
frequency ranges (Bates and Gregory, 2007).
The distinct frequency band of each signal means
that the spectral product in the above equation is zero. It also means
that
.
This frequency domain representation presents the opportunity
for decoding encoded signals by fdm,
where interfering signals are transmitted in several non-overlapping
frequency ranges (Bates and Gregory, 2007).
The distinct frequency band of each signal means
that the spectral product in the above equation is zero. It also means
that
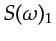 and
and
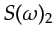 can be recovered by appropriate bandpass
filters applied to
can be recovered by appropriate bandpass
filters applied to  . One of FDM's most common applications is cable television,
where different TV channels are FDM encoded and sent over the cable simultaneously.
The decoding box at home then separates each channel from one another by decoding.
There are many other multiplexing schemes such as time-division, statistical, wavelength-division,
orthogonal frequency-division, code-division multiplexing (Bates and Gregory, 2007).
. One of FDM's most common applications is cable television,
where different TV channels are FDM encoded and sent over the cable simultaneously.
The decoding box at home then separates each channel from one another by decoding.
There are many other multiplexing schemes such as time-division, statistical, wavelength-division,
orthogonal frequency-division, code-division multiplexing (Bates and Gregory, 2007).
Yunsong Huang
2013-09-22
![]() is also considered signal, and the efficient transmission
of both signals requires that they both be simultaneously transmitted,
but should be separated from one another after recording1.1.
To achieve this feat, the two signals are encoded and summed together to give
is also considered signal, and the efficient transmission
of both signals requires that they both be simultaneously transmitted,
but should be separated from one another after recording1.1.
To achieve this feat, the two signals are encoded and summed together to give
![]() prior to transmission,
and then decoded
to get the separate signals
prior to transmission,
and then decoded
to get the separate signals
![]() and
and
![]() .
This efficient means of simultaneously transmitting two signals and their
subsequent decoding is a monumental achievement
because it greatly reduces both the
cost and the number of channels required for today's multi-channel communication.
.
This efficient means of simultaneously transmitting two signals and their
subsequent decoding is a monumental achievement
because it greatly reduces both the
cost and the number of channels required for today's multi-channel communication.
![]() is a device or operation1.2 that does
the reverse of the
is a device or operation1.2 that does
the reverse of the ![]() channel encoder, undoing the encoding so
that the original information can be retrieved.
An example in
digital electronics is where
a decoder can take the form of a multiple-input,
multiple-output logic circuit that
converts coded inputs into coded outputs.
Decoding is also necessary in applications such as data multiplexing,
which is seen in the oil industry with transmission
of multichannel seismic data.
channel encoder, undoing the encoding so
that the original information can be retrieved.
An example in
digital electronics is where
a decoder can take the form of a multiple-input,
multiple-output logic circuit that
converts coded inputs into coded outputs.
Decoding is also necessary in applications such as data multiplexing,
which is seen in the oil industry with transmission
of multichannel seismic data.
![]() is given by
is given by