If there are many signals added together and many crosstalk terms then
equation 1.3 can be generalized as
For seismic migration, equation 1.4 represents the migration image formed
by adding many shot gathers together and simultaneously migrating them. Unless the input
data is encoded, the
crosstalk term is too strong and spoils the image.
To reduce this spoilage
Morton and Ober (1998) encoded
their shot gathers by replacing the wavelet sources
with random times series, summing them together to form a supergather,
and migrating to give the migration image
where the encoding function
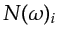 is
the spectrum of the
is
the spectrum of the  random time series
assigned to the
random time series
assigned to the  source. Each random time series
was selected to approximate the orthonormality condition
source. Each random time series
was selected to approximate the orthonormality condition
where
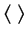 represents ensemble averaging,
which is another way of saying
that we should sum supergather migration images together, each with
a distinctly encoded supergather as the input data. Many other encoders have been proposed.
For example, Schuster et al. (2011) (see also references therein) showed that encoding the sources
with both random polarities and random phase shifts is better than encoding with either
scheme alone at reducing the crosstalk.
To make equation 1.6 approximately hold, more (say a factor
represents ensemble averaging,
which is another way of saying
that we should sum supergather migration images together, each with
a distinctly encoded supergather as the input data. Many other encoders have been proposed.
For example, Schuster et al. (2011) (see also references therein) showed that encoding the sources
with both random polarities and random phase shifts is better than encoding with either
scheme alone at reducing the crosstalk.
To make equation 1.6 approximately hold, more (say a factor 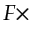 ) iterations are
required than the conventional migration.
As long as this overhead factor
) iterations are
required than the conventional migration.
As long as this overhead factor 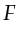 is less than the reduction factor--the number of sources included in a
supergather, this multisource endeavor leads to a speedup.
is less than the reduction factor--the number of sources included in a
supergather, this multisource endeavor leads to a speedup.
For the marine acquisition geometry, however, such crosstalk is troublesome.
The reason is that when 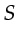 encoded shots are excited at nearly the same time the computer invariably simulates a supergather as in a land geometry with fixed receivers. In contrast, the actual marine shot gather is for a moving receiver string.
An example is shown in Fig. 1.1(c), where
the marine moving receiver string is denoted by the horizontal green bar at the top,
while the fixed receivers in the simulated
land geometry encompass the full width of the color-coded velocity model.
This implies that the computer-generated land shot gathers have too many traces per shot compared to the actual marine shot gather. Consequently, there will be a large residual,
encoded shots are excited at nearly the same time the computer invariably simulates a supergather as in a land geometry with fixed receivers. In contrast, the actual marine shot gather is for a moving receiver string.
An example is shown in Fig. 1.1(c), where
the marine moving receiver string is denoted by the horizontal green bar at the top,
while the fixed receivers in the simulated
land geometry encompass the full width of the color-coded velocity model.
This implies that the computer-generated land shot gathers have too many traces per shot compared to the actual marine shot gather. Consequently, there will be a large residual,
 , at the uncommon receiver locations, even if the true velocity model is used in the simulation.
Note that if there was
no crosstalk, i.e., if every receiver could tell apart its contributing sources, then the problem of erroneous residual would vanish, as will be explained in the next paragraph.
, at the uncommon receiver locations, even if the true velocity model is used in the simulation.
Note that if there was
no crosstalk, i.e., if every receiver could tell apart its contributing sources, then the problem of erroneous residual would vanish, as will be explained in the next paragraph.
A receiver in a multisource simulation would receive signals from all sources in a supershot, although in the marine case only a subset of sources are associated with this receiver. When free of crosstalk,
the receiver can determine what signals stem from the superfluous sources in simulation, and thus it can discount those signals before calculating the residual. In this way, no erroneous residual can arise.
Figure 1.1:
Overview of multisource frequency selection.
(a) Frequency-division multiplexing/demultiplexing used in telecommunication.
(b) Frequency-encoding three shot gathers to form a supergather, which is subsequently disentangled (indicated by the dashed lines) by frequency selection.
(c) FWI obtained by multisource frequency selection, with the resulting velocity model color-coded in the background, and
sine waves of different frequencies injected at different source locations. Color stars in (b, c) denote sources.
|
![\includegraphics[width=6in]{DissertationPPT/intro_figures}](img67.png) |
This begs the question whether in multisource seismic inversion there is a crosstalk-free encoding scheme.
Until now, in exploration geophysics no such scheme has been devised.
In this dissertation, I have designed a crosstalk-free encoding strategy, similar to
the fdm used in the communications industry, as depicted in Fig. 1.1(a).
The idea is to assign each shot gather to a unique set of frequencies. Careful
assignment ensures no overlap in frequencies from one shot
gather to the next, as illustrated in Fig. 1.1(a and b). That is,
the source signatures are orthogonal to each other, and so the cross-talk between sources is zero.
Using this scheme with marine streamer geometry is illustrated in Fig. 3.1 on page ![[*]](crossref.png) , and also in
in Fig. 1.1(c).
In Chapters 2 and 3, I show how this scheme, called `frequency selection' in this dissertation,
can be successfully
applied to multisource lsm and multisource fwi, respectively.
The benefit is that my numerical results show that for my examples, multisource imaging with frequency selection provides a speedup of more than
, and also in
in Fig. 1.1(c).
In Chapters 2 and 3, I show how this scheme, called `frequency selection' in this dissertation,
can be successfully
applied to multisource lsm and multisource fwi, respectively.
The benefit is that my numerical results show that for my examples, multisource imaging with frequency selection provides a speedup of more than 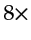 and
and 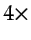 compared to conventional migration and fwi, respectively.
compared to conventional migration and fwi, respectively.
Yunsong Huang
2013-09-22
![]() encoded shots are excited at nearly the same time the computer invariably simulates a supergather as in a land geometry with fixed receivers. In contrast, the actual marine shot gather is for a moving receiver string.
An example is shown in Fig. 1.1(c), where
the marine moving receiver string is denoted by the horizontal green bar at the top,
while the fixed receivers in the simulated
land geometry encompass the full width of the color-coded velocity model.
This implies that the computer-generated land shot gathers have too many traces per shot compared to the actual marine shot gather. Consequently, there will be a large residual,
encoded shots are excited at nearly the same time the computer invariably simulates a supergather as in a land geometry with fixed receivers. In contrast, the actual marine shot gather is for a moving receiver string.
An example is shown in Fig. 1.1(c), where
the marine moving receiver string is denoted by the horizontal green bar at the top,
while the fixed receivers in the simulated
land geometry encompass the full width of the color-coded velocity model.
This implies that the computer-generated land shot gathers have too many traces per shot compared to the actual marine shot gather. Consequently, there will be a large residual,
![]() , at the uncommon receiver locations, even if the true velocity model is used in the simulation.
Note that if there was
no crosstalk, i.e., if every receiver could tell apart its contributing sources, then the problem of erroneous residual would vanish, as will be explained in the next paragraph.
, at the uncommon receiver locations, even if the true velocity model is used in the simulation.
Note that if there was
no crosstalk, i.e., if every receiver could tell apart its contributing sources, then the problem of erroneous residual would vanish, as will be explained in the next paragraph.
![\includegraphics[width=6in]{DissertationPPT/intro_figures}](img67.png)
![[*]](crossref.png) , and also in
in Fig. 1.1(c).
In Chapters 2 and 3, I show how this scheme, called `frequency selection' in this dissertation,
can be successfully
applied to multisource lsm and multisource fwi, respectively.
The benefit is that my numerical results show that for my examples, multisource imaging with frequency selection provides a speedup of more than
, and also in
in Fig. 1.1(c).
In Chapters 2 and 3, I show how this scheme, called `frequency selection' in this dissertation,
can be successfully
applied to multisource lsm and multisource fwi, respectively.
The benefit is that my numerical results show that for my examples, multisource imaging with frequency selection provides a speedup of more than