


Next: List of Tables
Up: Thesis
Previous: TABLE OF CONTENTS
Contents
- Hess salt models used in the TTI RTM test: distributions for the P-wave velocity (top),
epsilon (middle) and delta (bottom). Dip angle theta is constant and equals 30 degrees.
- TTI RTM images plotted with the background P-wave velocity model.
On the bottom is the TTI RTM image of the synthetic data generated with a 30 degrees tilt angle.
For comparison, the same data is migrated by conventional isotropic RTM and the result is shown on the top. The TTI RTM image matches the structure quite well,
but on the isotropic one, image blurring and mispositioning is present.
- Partial region of the 2D BP TTI model.
Top left shows the P-wave velocity distribution,
top right and the bottom left show the Thomsen anisotropy parameter model.
The bottom right is the input dip angle relative to the vertical symmetry.
- (a) is the gradient of the dip angle theta weighted by
.
(b) shows the filtered gradient by a given threshold.
White corresponds to 0 and black corresponds to 1.
Parameter equating of epsilon and delta is done along the black curve.
(c) and (d) are wavefield snapshots without and with
anisotropic parameter equating. Wavefield "blow up" is accommodated by
equating epsilon and delta around the high gradient points.
- The TTI RTM image (right) for the 2D BP TTI benchmark dataset.
Left panel shows the isotropic RTM image. The salt flank is well delineated by TTI RTM
but is mispositioned in the isotropic RTM image.
- Wavefield snapshots at time
 in a homogeneous TTI medium
(
in a homogeneous TTI medium
(
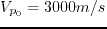 ,
,
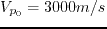 ,
,
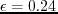 ,
,
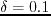 )
computed using different TTI equations.
(a) is generated from the TTI coupled equations with
)
computed using different TTI equations.
(a) is generated from the TTI coupled equations with 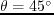 .
(b) is the same as (a) but with a nonzero SV wave velocity.
(c) and (d) are the results from the solution of the TTI decoupled P and SV wave equations, respectively.
.
(b) is the same as (a) but with a nonzero SV wave velocity.
(c) and (d) are the results from the solution of the TTI decoupled P and SV wave equations, respectively.
- Wavefield snapshots at time
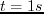 in a homogeneous TTI medium
(
in a homogeneous TTI medium
(
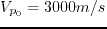 ,
,
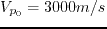 ,
,
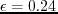 ,
,
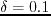 )
computed using different TTI equations.
(a) is generated from the TTI coupled equations with
)
computed using different TTI equations.
(a) is generated from the TTI coupled equations with 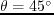 .
(b) is the same as (a) but with a nonzero SV wave velocity.
(c) and (d) are the results from the solution of the TTI decoupled P and SV wave equations, respectively.
.
(b) is the same as (a) but with a nonzero SV wave velocity.
(c) and (d) are the results from the solution of the TTI decoupled P and SV wave equations, respectively.
- Anisotropic parameter values of a 2D wedge model used in TTI modeling tests:
(a)
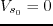 , (b)
, (b) 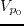 , (c)
, (c) 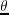 and (d)
and (d) 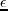 .
.
- Wavefield snapshots of the wedge model at time
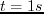 .
(a) shows the interface with sharp dip contrasts.
(b) The wavefield snapshot from the solution of the TTI coupled equations with
.
(a) shows the interface with sharp dip contrasts.
(b) The wavefield snapshot from the solution of the TTI coupled equations with 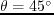 .
(c) Same as (b) but with a non-zero SV wave velocity.
(d) is computed by using the TTI decoupled P wave equation.
.
(c) Same as (b) but with a non-zero SV wave velocity.
(d) is computed by using the TTI decoupled P wave equation.
- The same plot as Figure 3.4 but the wavefield snapshots
are recorded at time
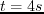 . (b) starts to blow up while (c) and (d) keep stable.
. (b) starts to blow up while (c) and (d) keep stable.
- Wavefield snapshots at time
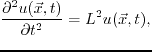 . The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
. The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
- Partial region of the 2D BP TTI model: (a)
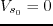 , (b)
, (b) 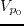 , (c)
, (c) 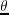 and (d)
and (d) 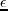 .
.
- Wavefield snapshots of the BP 2D TTI model.
(a) The gradient of dip angle model (displayed with an appropriate clip value)
where black line segments correspond to sharp dip contrasts in the dip model.
(b) The wavefield snapshot from the TTI coupled equations with
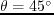 .
The instability problem arises from where high dip contrasts exist.
(c) The same as (b) but with a finite
.
The instability problem arises from where high dip contrasts exist.
(c) The same as (b) but with a finite 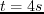 . The wavefield blow-up disappeared.
(d) The wavefield snapshot computed using the TTI decoupled P wave equation.
. The wavefield blow-up disappeared.
(d) The wavefield snapshot computed using the TTI decoupled P wave equation.
- Comparison of (a) VTI RTM and (b) TTI RTM images of the partial BP model.
- Zoom view of Figure 3.9.
(a)
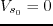 , (b) VTI RTM image and (c) TTI RTM image.
, (b) VTI RTM image and (c) TTI RTM image.
- Anisotropic model parameters used in the accuracy test.
- Three traces computed from the 2D 5-layer TTI model are displayed in wiggle mode.
(a) compares the first (strongest) reflection event, while (b) compares lower (weak) reflections.
- 2D 1-shot runtime comparison with different RTM shemes.
- TTI RTM image of the BP 2D TTI model.
- Actual reflectivity of the BP 2D TTI model.
- 3D salt dome models: a)
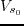 and b)
and b) 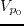 , c) and d) are Thomsen's parameters
, c) and d) are Thomsen's parameters 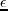 and
and
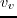 .
The front frame and side frame correspond to 2D slices at
.
The front frame and side frame correspond to 2D slices at 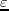 =
=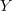
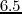 and
and 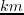 =
=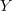
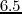 , respectively.
, respectively.
- 3D 1-shot runtime comparison with different RTM shemes.
- TTI RTM image of the 3D salt dome model.
- Wavefield snapshots at time
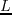 in a 3D homogeneous TTI medium
with
in a 3D homogeneous TTI medium
with
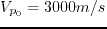 ,
,
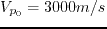 ,
,
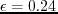 ,
,
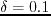 and
and
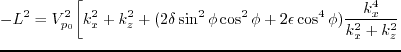 .
A point source is located in the center at
.
A point source is located in the center at
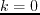 .
(a), (b) and (c) are 2D
.
(a), (b) and (c) are 2D 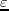 -
-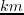 ,
, 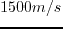 -
-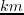 and
and 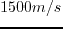 -
-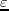 slices across the source location, respectively.
slices across the source location, respectively.
List of Tables
LIST OF TABLES
Ge Zhan
2013-07-09
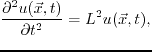 . The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
. The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
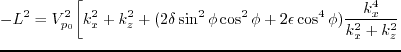 .
A point source is located in the center at
.
A point source is located in the center at
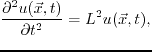 . The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
. The instabilities occur in both (b) and (c).
But wave propagation in (d) remains stable.
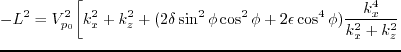 .
A point source is located in the center at
.
A point source is located in the center at