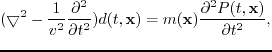Next: Migration of a Supergather
Up: Theory
Previous: Forward Modeling of a
Contents
In LSRTM, the Born modeling operator is used to fit the observed reflection data with a reflectivity model
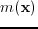 . Following Dai et al. (2012), the Born modeling of a supergather can be computed
in the time domain as
. Following Dai et al. (2012), the Born modeling of a supergather can be computed
in the time domain as
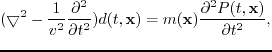 |
(39) |
subsequent to equation 3.7.
The frequency domain data
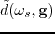 can be extracted from
can be extracted from
 according to
according to
 |
(310) |
Digitizing
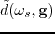 yields a supergather
yields a supergather
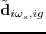 containing the reflection waves. Equations 3.7, 3.9, and 3.10 represent the numerical computation of the Born modeling operator
containing the reflection waves. Equations 3.7, 3.9, and 3.10 represent the numerical computation of the Born modeling operator
 in equation 3.3.
in equation 3.3.
Wei Dai
2013-07-10