Migration of a Supergather

The migration operator can be formulated as the adjoint of the Born modeling operator. Corresponding to equation 3.9, the migration formula is

$$(\bigtriangledown^{2}-\frac{1}{v^2}\frac{\partial^2}{\partial t^2... ...e[\tilde{d}(\omega_s,\textbf{g})e^{i\omega_s t}] \delta(\textbf{x}-\textbf{g}),$$ (311)

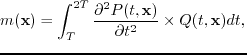$${m}(\textbf{x})=\int_T^{2T} \frac{\partial^2 {P}(t,\textbf{x})}{\partial t^2} \times {Q}(t,\textbf{x})dt,$$ (312)

where 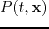${P}(t,\textbf{x})$ is the source wavefield obtained with equation 3.7, 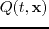${Q}(t,\textbf{x})$ is the receiver wavefield and equation 3.12 indicates a dot product imaging condition after both source and receiver wavefields reach steady state.

With the above definitions of the Born modeling and migration operators, the LSRTM scheme in Equation 3.4 can be implemented numerically. In the following examples, the preconditioned conjugate gradient method is used as the iterative solver.