Courses & Descriptions
ErSE 345: Seismic Interferometry
Seismic interferometry is an exciting field in geophysics utilising multiple scattering events to provide unprecedented views of the Earth's subsurface. This is a comprehensive course introducing the theory and practice of seismic interferometry with an emphasis on applications in exploration seismology.ErSE 290: Ambient Noise Seismology
This course presents the principles and practice of ambient noise seismology. Ambient noise seismology takes passive recordings of the earth's vibrations and transforms them into coherent seismic signals.
These signals consist of surface waves, body wave reflections, and backscattered events. The Reciprocity theorem is the underlying
theory, and we will apply it to passive data recorded by USArray data and a 10,000 station Long Beach array. The result will be used to estimate the subsurface reflectivity and velocity structures. We will
also design passive recording experiments and collect passive seismic data in KSA.
ErSE 260: Seismic Imaging
In seismic exploration, seismic imaging creates images of the subsurface using seismic waves generated by artificial sources (explosive sources or airguns) and recorded into extensive arrays of sensors (geophones or hydrophones). The technology is based on a complex, and rapidly evolving, mathematical theory that employs advanced solutions to a wave equation as tools to solve the general seismic inverse problem.
ErSE 328 & 329: Advanced Seismic Inversion
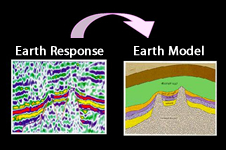Learn advanced inversion methods for reconstructing earth structure from seismic data: waveform inversion, image domain inversion, and
least squares migration. Non-linear optimization methods are introduced, which include gradient type methods of Newton, steepest descent, conjugate gradient and Quasi-Newton. To provide better stability and performance, preconditioning, regularization and multigridding methods are discussed. Resolution methods such as diffraction-slice theorem and generalized Radon Transform are used to determine the resolution of the reconstructed object.
ErSE 210: Seismology I
Learn fundamental physics and computational aspects of seismology as applied to exploration and earthquake geophysics. Topics inlcude derivation of acoustic and SH wave equations, plane wave and point source solutions; principles of Fermat, Snell, and Huygen; reflection+transmission coefficients; reciprocity equations; finite-difference solutions; convolution forward modeling; elastic wave equation; eikonal equation; surface waves; dispersion relationship; guided waves; earthquakes; head waves; diving waves; Green's functions; transport equation; and tomography. Fundamental theory of anisotropy,
including derivation of Christoffel matrix, Quasi-P, Quasi-SH, Quasi-SV
waves, Voit notation, VTI and Cubic symmetries.
ErSE 390a: Signal and Image Processing
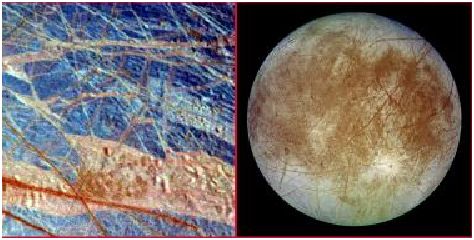Learn to filter and transform digital signals/images, apply processing methods to remote sensing and seismic data. Topics include Hilbert transform, 1D and 2D DFTs, deconvolution of vibroseis data,
median filters, PEFs, deconvolution, Z transform, edge detection,
wavelets.
ErSE 218: Geophysical Field Methods
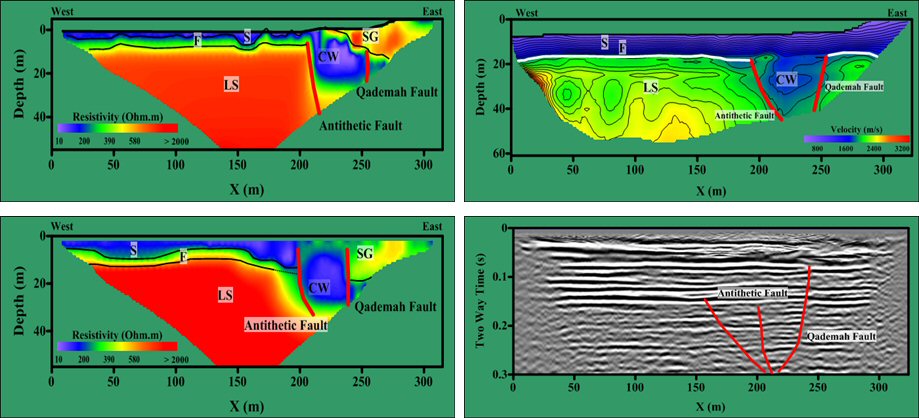Seismic refraction and reflection acquisition, processing, and interpretation, traveltime tomography. Resistivity VES and ERT acquisition and processing. Microgravity acquisition, correction, and processing. EM acquisition and interpretation.
ErSE 390b: Statistical and Deterministic Deconvolution
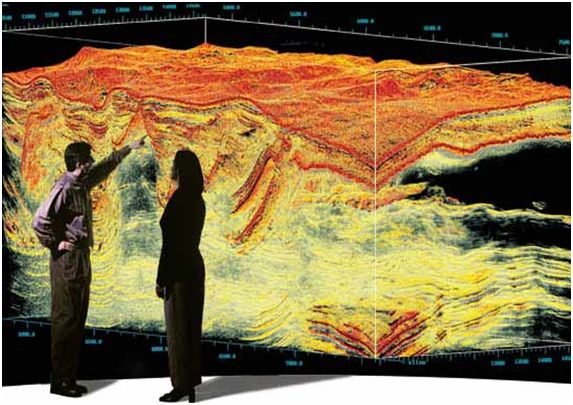The objective of the statistical and deterministic deconvolution short course is to familiarize exploration seismologists about the theory and practice of seismic deconvolution and zero-phase seismic processing. The prerequisite is a basic knowledge of vectors, matrices, and the Fourier transform. The course will consist of both lectures and in-class exercises, and topics to be covered include adaptive filtering,
migration decon, edge detection, 2D PEF, local filters,
and adaptive subtraction.
Short Courses
1-Day Rio Interferometry 2013 (Viewable Outline)
3-Day FWI and LSM
(Viewable Outline and Book to be published by SEG)
5-Day Petrobras-Amerada Hess Basic Seismology 2012, 2013 &
2014
(Outline, PPT,
and PDF Book)
5-Day Petrobras Interferometry 2011
(Viewable Outline, PPT overview, and PDF Book)
2-Day BP Seismic Imaging 2011
(Viewable Outline, PPT overview, and PDF Book )
1-Day EAGE London/Barcelona Interferometry 2010
(Viewable Outline, PPT overview and Book)
2-Day Norway Interferometry 2009
(Viewable Outline, PPT overview, and Book)
1-Day Belem Interferometry 2008 (Viewable Outline and Book)
3-Day Aramco Deconvolution+Migration (2002-2004)
(Viewable Outline
and PDF Book
)
4-Day Intermediate Tomography (2000)
(Viewable Outline)
2-Day Stanford Basics of Tomography (1998)
(Viewable Outline and HTML Book)
Advanced Finite Difference
Methods UU (1990-1991)