



Next: Introduction
Up: Generalized Diffraction-Stack Migration
Previous: Summary
Contents
Phase-encoded Wave-equation Migration
The theory for least-squares generalized diffraction-stack migration (LSGDM)
was presented in Chapter ![[*]](crossref.png) .
Now I test the performance of LSGDM using the phase-encoded multisource technology.
The key idea is, for an assumed velocity model, the receiver-side Green's function
and the source-side Green's function
are computed by a numerical solution of the wave equation.
The multisource migration operator is formed by convolution of these two Green's functions
followed by phase-encoding.
Recorded shot gathers are phase-encoded together with the same phase-encoding function to form a supergather.
Then the GDM image is obtained by an
.
Now I test the performance of LSGDM using the phase-encoded multisource technology.
The key idea is, for an assumed velocity model, the receiver-side Green's function
and the source-side Green's function
are computed by a numerical solution of the wave equation.
The multisource migration operator is formed by convolution of these two Green's functions
followed by phase-encoding.
Recorded shot gathers are phase-encoded together with the same phase-encoding function to form a supergather.
Then the GDM image is obtained by an 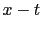 domain dot product between
the supergather and the multisource migration operator for every trial image point.
The dot product of unrelated migration operators and shot gathers
inevitably brings cross-talk noise into the migration image.
To deal with such noise, the least-squares algorithm is adopted.
Numerical results show that the LSGDM method combined with the phase-encoded multisource technology
can lead to an
efficient computation of wave equation least-squares migration (LSM) images
in almost the same time as that of conventional reverse-time migration (RTM).
It is especially suited to efficient target oriented migration.
domain dot product between
the supergather and the multisource migration operator for every trial image point.
The dot product of unrelated migration operators and shot gathers
inevitably brings cross-talk noise into the migration image.
To deal with such noise, the least-squares algorithm is adopted.
Numerical results show that the LSGDM method combined with the phase-encoded multisource technology
can lead to an
efficient computation of wave equation least-squares migration (LSM) images
in almost the same time as that of conventional reverse-time migration (RTM).
It is especially suited to efficient target oriented migration.
Subsections




Next: Introduction
Up: Generalized Diffraction-Stack Migration
Previous: Summary
Contents
Ge Zhan
2013-07-08
![[*]](crossref.png) .
Now I test the performance of LSGDM using the phase-encoded multisource technology.
The key idea is, for an assumed velocity model, the receiver-side Green's function
and the source-side Green's function
are computed by a numerical solution of the wave equation.
The multisource migration operator is formed by convolution of these two Green's functions
followed by phase-encoding.
Recorded shot gathers are phase-encoded together with the same phase-encoding function to form a supergather.
Then the GDM image is obtained by an
.
Now I test the performance of LSGDM using the phase-encoded multisource technology.
The key idea is, for an assumed velocity model, the receiver-side Green's function
and the source-side Green's function
are computed by a numerical solution of the wave equation.
The multisource migration operator is formed by convolution of these two Green's functions
followed by phase-encoding.
Recorded shot gathers are phase-encoded together with the same phase-encoding function to form a supergather.
Then the GDM image is obtained by an