Next: Filling in the Model Up: Model Resolution Function and Previous: Diffraction-Transmission Contents
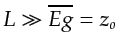 so we can approximate the
ellipse formula for the first Fresnel zone centering about
so we can approximate the
ellipse formula for the first Fresnel zone centering about 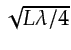 along the middle of the
Figure 4.8a wavepath.
This unexpectedly
high resolution limit near the reflector boundaries
can be observed in wave equation reflection traveltime (Zhang et al., 2012)
and migration velocity analysis (Zhang and Schuster, 2013) tomograms.
along the middle of the
Figure 4.8a wavepath.
This unexpectedly
high resolution limit near the reflector boundaries
can be observed in wave equation reflection traveltime (Zhang et al., 2012)
and migration velocity analysis (Zhang and Schuster, 2013) tomograms.
To illustrate the range of wavenumbers estimated from diffraction and transmission migration, Figures 4.9 depicts the low wavenumbers (magneta dots) of the model recovered with transmission migration (see Figure 4.7) and the higher wavenumbers (gray dots) recovered by diffraction migration (Figure 4.5). Note the large gap between the recovered low- and high- wavenumber spectra, which will be denoted as the missing intermediate wavenumbers. The abscence of such intermediate model wavenumbers is a serious challenge for waveform inversion (Jannane et al., 1989), which will be addressed in the next section.
![\includegraphics[width=4.2in,trim=40 0 0 30, clip]{figs/wavepath1/Fig1}](img470.png) |
Yunsong Huang 2013-09-22