How do the resolution characteristics
of the diffraction-transmission wavepaths in Figure 4.4d compare
to those for the reflection-transmission wavepaths in Figure 4.4b-c?
Figure 4.8 suggests that
the diffraction resolution limit
will be significantly better because the
diffraction propagation distance is effectively halved, leading
to a narrower wavepath.
This means that, if the waveform residuals are used to update
the velocity, then the diffraction updates
will have significantly better resolution
than the reflection updates.
The resolution limits for diffraction-transmission migration
can be quantified
according to equation 4.11,
which says that the maximum resolution limits perpendicular to
the diffraction and reflection central rays should be,
respectively,
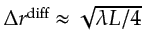 and
and
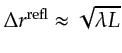 . In this case,
. In this case,
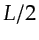 is
the effective length of the central ray between the geophone
and the scatterer in Figure 4.8a.
is
the effective length of the central ray between the geophone
and the scatterer in Figure 4.8a.
These limits can be rigorously derived by
defining the diffraction
Green's function
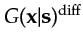 as
as
where
the diffractor is located
at
 , the trial image point is at
, the trial image point is at  ,
and
,
and
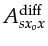 accounts for the effects of geometrical spreading,
reflection amplitude, and phase changes due to scattering.
Replacing the migration kernel
in equation 4.6 by
accounts for the effects of geometrical spreading,
reflection amplitude, and phase changes due to scattering.
Replacing the migration kernel
in equation 4.6 by
![$ [G({\bf{g}}\vert{\bf{x}})^{\textrm{diff}}G({\bf{x}}\vert{\bf{s}})^{\textrm{dir}}]^*$](img451.png) and the
data kernel by
and the
data kernel by
![$ [G({\bf {g}}\vert{\bf {y}})^{\textrm{diff}}G({\bf {y}}\vert{\bf {s}})^{\textrm{dir}}]$](img459.png) ,
and using the explicit expression for
the Green's functions yields
the model resolution function for diffraction imaging:
,
and using the explicit expression for
the Green's functions yields
the model resolution function for diffraction imaging:
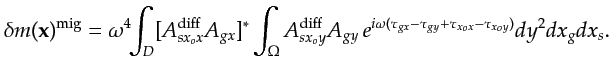 |
(4.15) |
The salient difference between this formula and the one
for reflections in equation F.4
is that
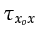 and
and
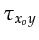 replace
replace 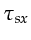 and
and  .
This says that the diffraction wavepath
is generated by a ``virtual'' source
at the diffractor
.
This says that the diffraction wavepath
is generated by a ``virtual'' source
at the diffractor
 rather than at the
actual source location
rather than at the
actual source location  . Hence, the diffraction
wavepath should be thinner than the specular reflection wavepath in Figure 4.8.
In addition, every source-geophone pair has
a diffraction wavepath that intersects the
the diffractor. This means that, similar to diffraction migration, many more diffraction wavenumbers will be available for velocity updates
compared to specular reflection-transmission wavepaths.
. Hence, the diffraction
wavepath should be thinner than the specular reflection wavepath in Figure 4.8.
In addition, every source-geophone pair has
a diffraction wavepath that intersects the
the diffractor. This means that, similar to diffraction migration, many more diffraction wavenumbers will be available for velocity updates
compared to specular reflection-transmission wavepaths.
Yunsong Huang
2013-09-22
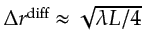 and
and
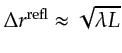 . In this case,
. In this case,
![]() is
the effective length of the central ray between the geophone
and the scatterer in Figure 4.8a.
is
the effective length of the central ray between the geophone
and the scatterer in Figure 4.8a.
![\includegraphics[width=4.5in]{figs/wavepath1/figfrez3}](img453.png)