The forward and adjoint modeling equations can be combined
to give the equation for model resolution, i.e.,
plugging equation 4.3 into equation 4.5
gives
 |
(4.6) |
or in more compact notation
The kernel for the operator
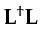 is related to the
model resolution matrix (Menke, 1989) and is interpreted as the point spread
function (Schuster and Hu, 2000) similar to
that used in optics, except here, if
is related to the
model resolution matrix (Menke, 1989) and is interpreted as the point spread
function (Schuster and Hu, 2000) similar to
that used in optics, except here, if
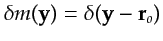 , it is
the migration response to a point slowness perturbation
in the model at
, it is
the migration response to a point slowness perturbation
in the model at
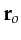 . The ideal response to a point
slowness anomaly is the same point with perfect resolution.
. The ideal response to a point
slowness anomaly is the same point with perfect resolution.
For a two-layer medium, the above Green's function can be decomposed into its direct and reflection components:
where
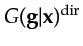 and
and
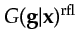 are the, respectively,
Green's function for the direct wave and upgoing reflection
in the upper layer.
Inserting equation 4.8 into the migration kernel in equation 4.6 results in the five migration kernels shown in Figure 4.4, each of which is used to
smear residuals along one of the five yellow-colored wavepaths (Liu et al., 2011; Zhan et al., 2013).
are the, respectively,
Green's function for the direct wave and upgoing reflection
in the upper layer.
Inserting equation 4.8 into the migration kernel in equation 4.6 results in the five migration kernels shown in Figure 4.4, each of which is used to
smear residuals along one of the five yellow-colored wavepaths (Liu et al., 2011; Zhan et al., 2013).
Subsections
Yunsong Huang
2013-09-22