Next: Diffraction-Transmission Up: Model Resolution Equation: Previous: Diving-Wave Transmission Contents
The corresponding model resolution formula for the rightmost rabbit-ear wavepath is
Estimating the resolution limits for the rabbit-ear wavepaths
will result in model resolution formulas similar to that given in Figure 4.4a for transmission imaging. This can be understood without
going through the detailed algebra by
recognizing that the upgoing reflection wavepath (rightmost rabbit ear in Figure 4.1a) is identical to
the transmission wavepath in Figure 4.1b above the
interface. This is denoted as a mirror
transmission wavepath because it coincides with the first Fresnel
zone for a source
at the mirror position ![]() in a homogeneous velocity.
Thus, the reflection traveltime in a) is
identical to the transmission traveltime in b)
for any receiver at
in a homogeneous velocity.
Thus, the reflection traveltime in a) is
identical to the transmission traveltime in b)
for any receiver at
![]() .
This means that
the resolution limits defined by equation 4.2
are applicable to the transmission wavepaths in
Figure 4.1b and the
reflection wavepaths in Figure 4.1a.
However, the range of available wavenumbers for
the traces recorded at
.
This means that
the resolution limits defined by equation 4.2
are applicable to the transmission wavepaths in
Figure 4.1b and the
reflection wavepaths in Figure 4.1a.
However, the range of available wavenumbers for
the traces recorded at ![]() is determined
by the limited range of sources in Figure 4.6a
that allow for the intersection of their
first Fresnel zones with the scatterer.
For example, the resolution limit
is determined
by the limited range of sources in Figure 4.6a
that allow for the intersection of their
first Fresnel zones with the scatterer.
For example, the resolution limit
![]() perpendicular to the ray at the
midpoint should be equal to the
perpendicular to the ray at the
midpoint should be equal to the
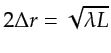 in Figure 4.1a, except the total length of the reflection ray is
in Figure 4.1a, except the total length of the reflection ray is
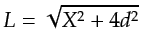 .
.
Yunsong Huang 2013-09-22