Reflection migration smears
residuals along the yellow-colored ellipse in
Figure 4.4e for a specified source and receiver pair.
When two traces
are migrated, Figure 4.3b suggests that the minimum
width and height of the intersecting fat ellipses
defines the resolution limits of reflection migration.
The formulas for migration resolution limits were more rigorously
derived (Beylkin, 1985) by
applying the migration kernel to
traces that only contain the diffraction arrival
from a single diffractor. For a localized
scatterer4.3in a background medium with smooth velocity variations, Beylkin showed that
equation 4.6 asymptotically becomes
the Fourier integral over the model wavenumbers 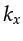 and
and 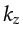 :
:
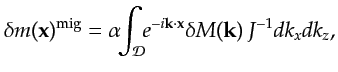 |
(4.9) |
where 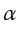 is related to geometrical spreading,
is related to geometrical spreading, 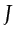 is the Jacobian,
which is derived in Appendix G,
and the range of model wavenumbers
is the Jacobian,
which is derived in Appendix G,
and the range of model wavenumbers
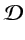 in the integral
depends on the range of source-receiver pairs.
In fact,
the model wavenumber vector
in the integral
depends on the range of source-receiver pairs.
In fact,
the model wavenumber vector  can
be equated to the sum of the source-scatterer
and geophone-scatterer wavenumbers
can
be equated to the sum of the source-scatterer
and geophone-scatterer wavenumbers
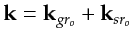 shown in Figure 4.5.
I will now show how equations 4.6
and 4.9 can be used to estimate the resolution limits of the other wavepaths in Figure 4.4a-d.
shown in Figure 4.5.
I will now show how equations 4.6
and 4.9 can be used to estimate the resolution limits of the other wavepaths in Figure 4.4a-d.
Yunsong Huang
2013-09-22
![]() and
and ![]() :
: