



Next: Introduction
Up: Generalized Diffraction-Stack Migration
Previous: Contents
Contents
- Simple diffraction-stack migration operator (red hyperbola) superimposed on the data, which only
accounts first arrival scattering information.
- The standard reverse-time migration (RTM) image is obtained by computing the
zero-lag correlation of the forward-propagated source wavefield a) with the back-projected data b). The scattering point at
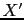 shows up in c) after
applying the imaging condition.
shows up in c) after
applying the imaging condition.
- Formation of the GDM kernel.
a). Migration kernel
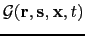 for a fixed image point at
for a fixed image point at 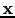 decomposed into the two modeling kernels: b) one
decomposed into the two modeling kernels: b) one
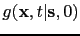 for a source at
for a source at  and the c) other
and the c) other
 for a source at
for a source at 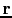 .
Convolving the
trace in b) with the trace in c) gives the far-right trace shown in a).
The other traces in a) represent the migration kernels at
other receiver positions.
.
Convolving the
trace in b) with the trace in c) gives the far-right trace shown in a).
The other traces in a) represent the migration kernels at
other receiver positions.
- Generalized diffraction-stack migration operator
(colored hyperbolas) which contains all events in the migration model, including multiples,
diffractions and reflections.
- Horizontal and vertical reflector models on the left
along with their associated wavepaths (Woodward, 1992) to the right.
a) shows the horizontal reflector model,
and its wavepaths in b) take the shapes of
a cigar, rabbit ears, and an elliptical smile.
c) and d) are the vertical reflector model and its corresponding wavepaths.
The wavepaths were computed by
migrating a single trace excited
by a wideband point source (star) and recorded at the receiver (quadrilateral).
- Raypaths associated with the products in
![$ [D^{t}({\bf{x}}\vert{\bf{r}})+U^{r}({\bf{x}}\vert{\bf{r}})]$](img53.png)
![$ [D^{t}({\bf{x}}\vert{\bf{s}})+U^{r}({\bf{x}}\vert{\bf{s}})]$](img54.png) .
The phase of these products at certain trial image points
.
The phase of these products at certain trial image points 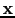 will annihilate the phase
in the data for
either
will annihilate the phase
in the data for
either
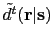 or
or
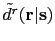 , but not both. The diving ray in a)
can lead to strong artifacts in the RTM image.
, but not both. The diving ray in a)
can lead to strong artifacts in the RTM image.
- Wavepaths in Figure
![[*]](crossref.png) b separated by dip filtering the migration
kernel
b separated by dip filtering the migration
kernel
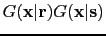 associated
with the horizontal reflector model in Figure
associated
with the horizontal reflector model in Figure ![[*]](crossref.png) a
(see the kernels in equation
a
(see the kernels in equation ![[*]](crossref.png) ).
).
- Wavepaths in Figure
![[*]](crossref.png) d separated by dip filtering the migration
kernel
d separated by dip filtering the migration
kernel
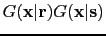 associated
with the vertical reflector model in Figure
associated
with the vertical reflector model in Figure ![[*]](crossref.png) c.
c.
- RTM results associated with the salt model.
a) Salt velocity model overlaid by the raypath of a single source-receiver pair.
b), c) and d) are RTM images of this model.
Shallow part of the image is overwhelmed by strong artifacts.
A high-pass filter is effective in suppressing these artifacts
but large residuals still remain.
- Up-down separation of Green's function. a) shows the model.
b) is the Green's function recorded along the vertical receiver line.
It is then filtered into c) upgoing and d) downgoing components.
- Left-right separation of Green's function. a) shows the model.
b) is the Green's function recorded along the horizontal receiver line.
It is then filtered into c) leftgoing and d) rightgoing components.
- Applying the Kirchhoff-like migration kernels
in equations
![[*]](crossref.png) and
and ![[*]](crossref.png) to recorded data gives, respectively, a) and b).
Stacking a) and b) gives c).
d) is the standard RTM image.
to recorded data gives, respectively, a) and b).
Stacking a) and b) gives c).
d) is the standard RTM image.
- Applying the Kirchhoff-like migration kernels
in equations
![[*]](crossref.png) and
and ![[*]](crossref.png) to all 126 shot gathers gives, respectively, a) and b).
c) is the stacking image of a) and b).
The high-pass filtered RTM image is shown in d).
to all 126 shot gathers gives, respectively, a) and b).
c) is the stacking image of a) and b).
The high-pass filtered RTM image is shown in d).
- The migration velocity and the standard RTM image of the Gulf of Mexico data set.
- The GDM image in comparison with the filtered RTM image.
The white dashed box highlights the differences of the two images.
- Migration kernels plotted in data space as colored hyperbolas for
a) primary and b) primary+multiple events
associated with shallow (green) and deep (pink) trial image points.
The best match between the data (black hyperbolas)
and migration curves (pink and green) is when the trial image point
is near the actual scatterer's position; the
dot-product between the migration kernel and data
fingerprints will give the greatest value when the trial image point is at the actual scatterer's location.
- Synthetic velocity model and associated shot gather.
a) is the fan model, with the background
velocity (gray color) of
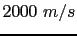 and the perturbed velocity (white color) of
and the perturbed velocity (white color) of 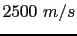 .
b) shows a typical shot gather at
.
b) shows a typical shot gather at 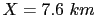 .
.
- Kirchhoff migration (KM) examples.
- Reverse-time migration (RTM) examples.
- Velocity model used in the synthetic tests.
- Synthetic Green's function and its separation in time.
a) A typical bandlimited Green's function generated from the 2D SEG/EAGE salt model.
The dashed box shows b) the early-arrivals.
c) The Green's function only containing multiples.
- Migration results using the GDM method.
a) Migration image constructed from migration kernel formed by convolving the early-arrivals.
b) Migration image using all of the arrivals to form a migration kernel.
c) Migration image using only multiples in the migration kernel.
d) The optimal stack of a) and c).
- Diffraction-stack migration versus generalized diffraction-stack migration.
a) Simple diffraction-stack migration operator (dashed hyperbola) and data, which only contains first arrival scattering
information. b) Generalized diffraction-stack migration operator (dashed hyperbolas) which contains all events in the
migration model, including multiples, diffractions and reflections.
- The 2D SEG/EAGE velocity model.
- Migration results for all 162 shot gathers of the SEG/EAGE salt model: a) GDM result which is identical to
standard RTM image; b) low cut filtered version of a); c) skeletonized least-squares GDM image after 10 iterations.
- Zoom view of the migration results. a) shows the true model, b) and c)
are the GDM results before and after least-squares iterations.
- The 2D SEG/EAGE velocity model and the corresponding reflectivity model.
- Comparison of single-source GDM results using the first-arrival Green's function.
- Comparison of single-source GDM results using the full Green's function.
- Formation of phase-encoded supergathers with different phase-encoding functions.
- Comparison of multisource GDM results without iterations using the first-arrival Green's function
and the full Green's function. Ten shot gathers are phase-encoded in a supergather
using source statics phase-encoding.
- Comparison of multisource GDM results without and with applying receiver statics.
- Comparison of multisource GDM results without and with applying random polarity.
- The least-squares phase-encoded GDM image after 20 iterations(b) with the starting model of (a).
(c) is the least-squares GDM image after 20 iterations without phase-encoding which is 10 times slower than (b).
Source and receiver statics and random polarity are all employed in this test.
acknowledgeAcknowledgments
Ge Zhan
2013-07-08
![[*]](crossref.png) b separated by dip filtering the migration
kernel
b separated by dip filtering the migration
kernel
![[*]](crossref.png) a
(see the kernels in equation
a
(see the kernels in equation ![[*]](crossref.png) ).
).
![[*]](crossref.png) d separated by dip filtering the migration
kernel
d separated by dip filtering the migration
kernel
![[*]](crossref.png) c.
c.
![[*]](crossref.png) and
and ![[*]](crossref.png) to recorded data gives, respectively, a) and b).
Stacking a) and b) gives c).
d) is the standard RTM image.
to recorded data gives, respectively, a) and b).
Stacking a) and b) gives c).
d) is the standard RTM image.
![[*]](crossref.png) and
and ![[*]](crossref.png) to all 126 shot gathers gives, respectively, a) and b).
c) is the stacking image of a) and b).
The high-pass filtered RTM image is shown in d).
to all 126 shot gathers gives, respectively, a) and b).
c) is the stacking image of a) and b).
The high-pass filtered RTM image is shown in d).